Tutorial: Simulate a model binary#
This tutorial walks through the basics of using phitter to compute light curves and RVs for a model stellar binary.
Imports#
from phitter import observables, filters
from phitter.params import star_params, binary_params, blackbody_params
from phitter.calc import model_obs_calc
import numpy as np
from phoebe import u
from phoebe import c as const
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
# The following warning regarding extinction originates from SPISEA and can be ignored.
# The functionality being warned about is not used by SPISEA.
/Users/abhimat/Software/miniforge3/envs/phoebe_py38/lib/python3.8/site-packages/pysynphot/locations.py:345: UserWarning: Extinction files not found in /Volumes/Noh/models/cdbs/extinction
warnings.warn('Extinction files not found in %s' % (extdir, ))
Set up observation filters / passbands#
For this example, we’re going to generate photometry and RVs in Keck Kp band. Any passband set up in both PHOEBE and SPISEA can be used by Phitter for simulating fluxes and RVs.
filter_kp = filters.nirc2_kp_filt()
Set up stellar and binary system parameters#
Stellar parameters#
We’re going to set up parameters for the component stars in the binary system with photometry derived from a blackbody. This requires providing mass, radius, and temperature for each star.
# Star parameters
bb_stellar_params_obj = blackbody_params.bb_stellar_params()
star1_params = bb_stellar_params_obj.calc_star_params(
50 * u.solMass, 52 * u.solRad, 30_000 * u.K,
)
star2_params = bb_stellar_params_obj.calc_star_params(
45 * u.solMass, 45 * u.solRad, 25_000 * u.K,
)
Set up a binary parameters object#
A separate object is set up to specify the parameters of the binary system
# Binary parameters
bin_params = binary_params.binary_params(
period = 20.0 * u.d,
ecc = 0.05,
inc = 80.0 * u.deg,
t0 = 53_800.0,
)
Set up of observables to be calculated#
We need to set up an observables object to specify the times and types of observables that need to be computed. For this example, let’s compute flux in Keck K-band and RVs uniformly over the entire orbital phase of the binary.
# Set up model times
# Model times are in MJD here
model_phases = np.linspace(0, 1, num=100)
model_times = model_phases * bin_params.period.value + bin_params.t0
# Set up filter and observation type arrays for the model fluxes and RVs
kp_filt_arr = np.full(len(model_phases), filter_kp)
kp_type_arr = np.full(len(model_phases), 'phot')
rv_pri_filt_arr = np.full(len(model_phases), filter_kp)
rv_pri_type_arr = np.full(len(model_phases), 'rv_pri')
rv_sec_filt_arr = np.full(len(model_phases), filter_kp)
rv_sec_type_arr = np.full(len(model_phases), 'rv_sec')
# Now make arrays for all the times, filters, and observation types by concatenating the above arrays
obs_times = np.concatenate(
(model_times, model_times, model_times),
)
obs_filts = np.concatenate(
(kp_filt_arr, rv_pri_filt_arr, rv_sec_filt_arr,),
)
obs_types = np.concatenate(
(kp_type_arr, rv_pri_type_arr, rv_sec_type_arr,),
)
# Finally, construct the observables object
model_observables = observables.observables(
obs_times=obs_times,
obs_filts=obs_filts, obs_types=obs_types,
)
Compute the observables#
First a model observation calculation object (model_obs_calc) has to be instantiated, with the observables as input parameters. This object will be carrying out the calculations.
# Object to perform the computation of flux and RVs
binary_model_obj = model_obs_calc.binary_star_model_obs(
model_observables,
use_blackbody_atm=True,
print_diagnostics=False,
)
The modeled observables can then be simulated by inputting the stellar and binary parameters.
modeled_observables = binary_model_obj.compute_obs(
star1_params, star2_params, bin_params,
)
Process and plot the modeled observables#
We can extract the different observables (flux and RVs of the primary and secondary object) from the output observables object. The observables object has numpy filters for each passband and data types that we can use for this.
# Fluxes in mags
modeled_kp_mags = modeled_observables.obs[modeled_observables.phot_filt_filters[filter_kp]]
print(f'Kp-band mags: {modeled_kp_mags}')
# RVs in km/s
modeled_rvs_star1 = modeled_observables.obs[modeled_observables.obs_rv_pri_filter]
modeled_rvs_star2 = modeled_observables.obs[modeled_observables.obs_rv_sec_filter]
print(f'Star 1 RVs: {modeled_rvs_star1} km/s')
print(f'Star 2 RVs: {modeled_rvs_star2} km/s')
Kp-band mags: [-7.5216657 -7.53732926 -7.5216657 -7.53973471 -7.58422804 -7.6434513
-7.70671535 -7.76850532 -7.82567567 -7.87684326 -7.92123227 -7.9589559
-7.98949251 -8.01222054 -8.02392512 -8.02926534 -8.03464135 -8.03978097
-8.04512171 -8.05026785 -8.05499389 -8.05965313 -8.06381118 -8.06742234
-8.0707711 -8.07336674 -8.0753406 -8.07691355 -8.07784988 -8.07791415
-8.07786586 -8.07681172 -8.07544044 -8.07313791 -8.0702784 -8.06746169
-8.0638797 -8.05981414 -8.05567433 -8.05147333 -8.04686716 -8.04234265
-8.03770362 -8.03263123 -8.0182408 -7.99586114 -7.96713968 -7.93223797
-7.89169488 -7.8463103 -7.79686441 -7.74500755 -7.69428287 -7.65015828
-7.62135114 -7.61633102 -7.63662295 -7.6757046 -7.7243426 -7.77576576
-7.82591875 -7.8724258 -7.91454599 -7.95108773 -7.98218025 -8.00744218
-8.0265221 -8.0384456 -8.04556605 -8.05304594 -8.06062383 -8.06820929
-8.0752654 -8.08167704 -8.08702932 -8.09139645 -8.09415882 -8.09548854
-8.09522449 -8.09383937 -8.09062861 -8.08629899 -8.08040402 -8.0734608
-8.0655998 -8.05723694 -8.04857565 -8.03984411 -8.03170232 -8.02326546
-8.00664823 -7.98281403 -7.95231821 -7.91482576 -7.87066209 -7.81978953
-7.76289086 -7.70152922 -7.63835483 -7.5803122 ]
Star 1 RVs: [ 8.3645588 -20.72126128 -42.78321712 -57.33403586 -66.82057916
-73.40743418 -78.48141781 -82.79790172 -86.81473427 -90.87297976
-95.17329818 -99.99513811 -106.16950658 -113.14473386 -119.59989517
-125.55295565 -130.9919105 -135.88108371 -140.29568743 -144.16538332
-147.52139283 -150.36323497 -152.68049597 -154.49586261 -155.82593365
-156.57922333 -156.8680753 -156.64458017 -155.90614339 -154.67592131
-152.94370496 -150.70965628 -147.98012086 -144.7153373 -140.9567258
-136.76601174 -132.00254521 -126.75365832 -121.01008446 -114.81700743
-108.12273938 -100.99997401 -93.39910259 -85.3842781 -76.97976576
-68.19792792 -59.04069552 -49.57086978 -39.81711275 -29.78706422
-19.55885966 -9.12678602 1.43364637 12.08601054 22.81407832
33.53972245 44.20659904 54.80346614 65.23094339 75.44727086
85.41728951 95.06716457 104.33120411 113.18878257 121.53341727
129.32082842 136.53697068 143.07943596 148.97988595 154.18420839
158.71292283 162.53692469 165.69212759 168.21006382 170.04745492
171.21145367 171.69995938 171.45932309 170.53705681 168.93993298
166.63771821 163.6308055 159.89544385 155.42984771 150.22590561
144.2864683 137.58360979 130.33004141 124.0580466 118.38509998
113.12074107 108.10089376 103.18221374 98.07183948 92.31597699
85.15214354 75.16779889 60.16406811 37.64145169 8.3645588 ] km/s
Star 2 RVs: [ -9.30041204 2.50410814 14.16562647 25.67206929 36.94494359
47.97531301 58.69174249 69.12035131 79.16694275 88.81417575
98.04413382 106.83285253 115.15213351 122.9893872 130.30413878
137.10017692 143.35255178 149.07128874 154.20704145 158.79735648
162.80580603 166.2663088 169.10218567 171.38539398 173.06966805
174.16508265 174.6643893 174.57883199 173.89271835 172.63868982
170.74759035 168.30877263 165.28297836 161.68059288 157.46400701
152.71996893 147.38982022 141.50576497 135.06435162 128.10485559
120.60515754 112.70100092 106.69837965 101.79244882 97.47733391
93.4133502 89.33096789 84.87011687 79.39775618 71.8552754
60.31299594 41.65245503 13.26456234 -21.70464555 -53.21215397
-75.12448441 -88.92807004 -97.94153472 -104.53558441 -109.95958671
-114.98414704 -119.97830835 -125.2164007 -130.86963335 -137.18480064
-144.68052272 -152.87248756 -160.38885062 -167.16675609 -173.20117313
-178.45298833 -182.88248841 -186.48124599 -189.23931305 -191.19961314
-192.243635 -192.49423607 -191.85823293 -190.38154407 -188.05011772
-184.87109601 -180.90651511 -176.11474404 -170.55151307 -164.21340472
-157.14966866 -149.38135158 -140.9742126 -131.96817453 -122.39822833
-112.33723958 -101.83936398 -90.97014566 -79.7680786 -68.32052664
-56.69329864 -44.903312 -33.03154919 -21.13607745 -9.30041204] km/s
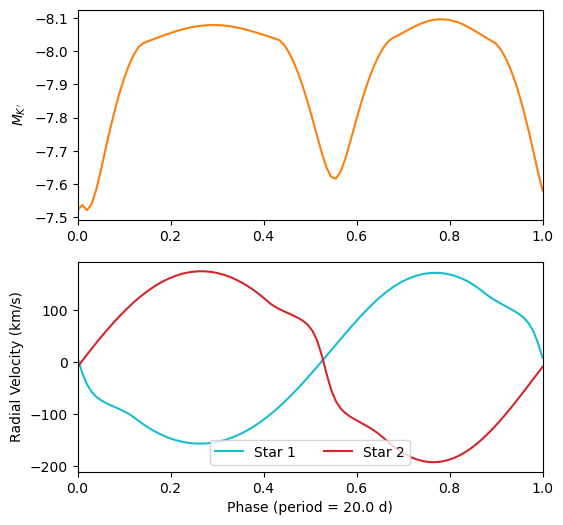
Now that we have the modeled observables, we can plot them for this model binary
fig = plt.figure(figsize=(6,6))
# Kp mags subplot
ax_mag_kp = fig.add_subplot(2,1,1)
ax_mag_kp.plot(
model_phases, modeled_kp_mags,
'-', color='C1',
)
ax_mag_kp.set_xlim([0, 1])
ax_mag_kp.invert_yaxis()
ax_mag_kp.set_ylabel(r"$M_{K'}$")
# RVs subplot
ax_rvs = fig.add_subplot(2,1,2)
ax_rvs.plot(
model_phases, modeled_rvs_star1,
'-', color='C9', label='Star 1',
)
ax_rvs.plot(
model_phases, modeled_rvs_star2,
'-', color='C3', label='Star 2',
)
ax_rvs.set_xlabel(f"Phase (period = {bin_params.period:.1f})")
ax_rvs.set_xlim([0, 1])
ax_rvs.set_ylabel("Radial Velocity (km/s)")
ax_rvs.legend(loc='lower center', ncol=2)
<matplotlib.legend.Legend at 0x16c180100>
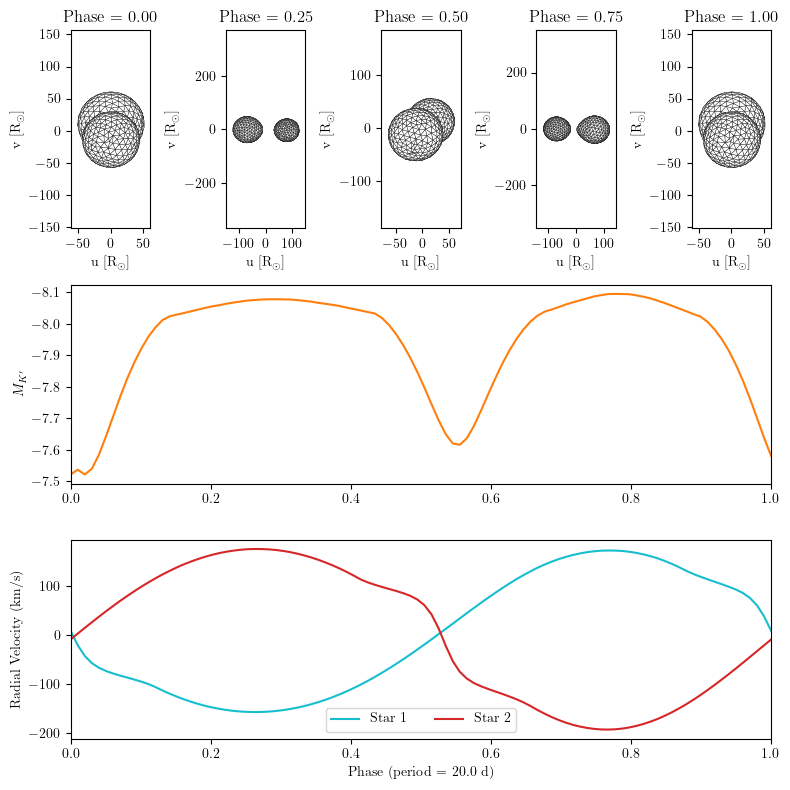
Bonus: make mesh plots to aide visualization#
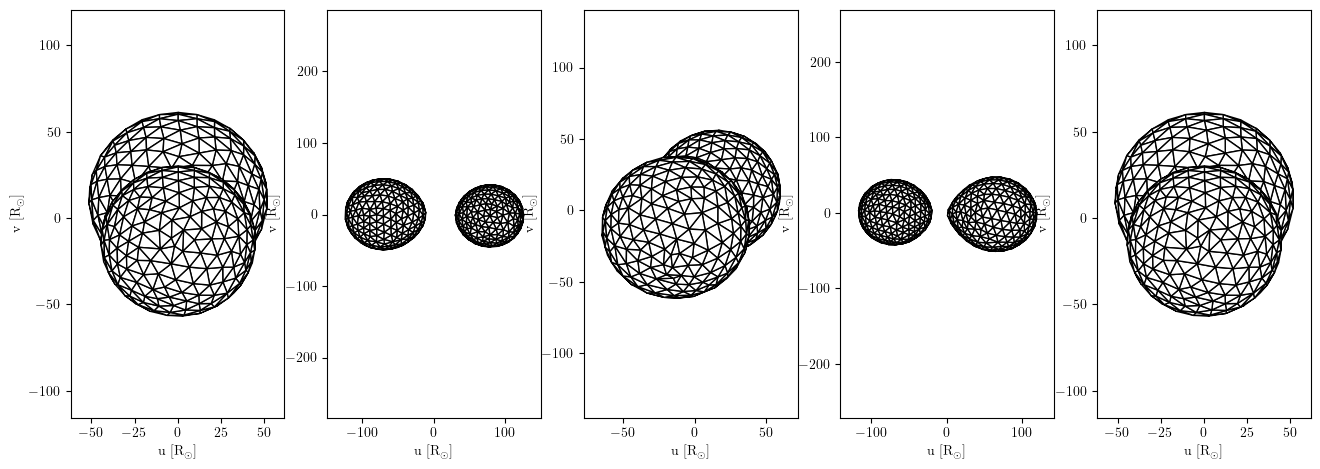
The above plot is great to see the modeled observables. But it can be helpful to see what the modeled binary system looks like. Let’s add simulate some mesh outlines of the stellar surfaces to see what this model binary looks like…
We need to make a figure first where we’ll do the plotting. We can be extra specific about the layout of the mesh plots in this figure, so let’s do that!
# Set up figure and specificy mesh plot outputs
fig = plt.figure(figsize=(8,8))
gs = plt.GridSpec(5, 5,)
mesh_plot_phases = np.array([0.0, 0.25, 0.5, 0.75, 1.0])
modeled_observables, mesh_plot_out, fig = binary_model_obj.compute_obs(
star1_params, star2_params, bin_params,
make_mesh_plots=True,
mesh_plot_phases=mesh_plot_phases,
mesh_plot_fig=fig,
mesh_plot_subplot_grid=(3,5),
mesh_plot_subplot_grid_indexes=np.array([1, 2, 3, 4, 5,]),
num_triangles=500,
)
# The mesh subplots show here since we have matplotlib inline enabled
# Finish constructing the whole figure
# Fluxes in mags
modeled_kp_mags = modeled_observables.obs[modeled_observables.phot_filt_filters[filter_kp]]
# RVs in km/s
modeled_rvs_star1 = modeled_observables.obs[modeled_observables.obs_rv_pri_filter]
modeled_rvs_star2 = modeled_observables.obs[modeled_observables.obs_rv_sec_filter]
# Label the mesh subplots
# # Remove empty axes
# for ax in fig.axes:
# if ax.get_xlabel() == '':
# ax.remove()
# # Make mesh axes share axes
# mesh_axes = []
for ax_index, phase in enumerate(mesh_plot_phases):
ax = fig.axes[ax_index]
ax.set_title(f'Phase = {phase:.2f}')
# Decrease linewidths of the triangles in the mesh, for legibility in final plot
for child in ax.get_children():
if isinstance(child, mpl.collections.PolyCollection):
child.set(lw=0.25)
# mesh_axes.append(ax)
# Draw observables subplots
# Kp mags subplot
ax_mag_kp = fig.add_subplot(3,1,2)
ax_mag_kp.plot(
model_phases, modeled_kp_mags,
'-', color='C1',
)
ax_mag_kp.set_xlim([0, 1])
ax_mag_kp.invert_yaxis()
ax_mag_kp.set_ylabel(r"$M_{K'}$")
# RVs subplot
ax_rvs = fig.add_subplot(3,1,3)
ax_rvs.plot(
model_phases, modeled_rvs_star1,
'-', color='C9', label='Star 1',
)
ax_rvs.plot(
model_phases, modeled_rvs_star2,
'-', color='C3', label='Star 2',
)
ax_rvs.set_xlabel(f"Phase (period = {bin_params.period:.1f})")
ax_rvs.set_xlim([0, 1])
ax_rvs.set_ylabel("Radial Velocity (km/s)")
ax_rvs.legend(loc='lower center', ncol=2)
fig.set_size_inches(8, 8)
fig.tight_layout()
fig