Tutorial: Simulate a model binary using stellar parameters from an isochrone#
Phitter allows interpolating the stellar parameters in a model binary system from MIST isochrones.
This may be useful if the age of a binary or the host star population is well constrained. In these cases, all stellar parameters necessary for successful light curve calculation don’t need to be specified: Phitter can interpolate along the MIST isochrone given just one parameter for a star (e.g.: initial mass).
Imports#
from phitter import observables, filters
from phitter.params import star_params, binary_params, isoc_interp_params
from phitter.calc import model_obs_calc
import numpy as np
from phoebe import u
from phoebe import c as const
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
# The following warning regarding extinction originates from SPISEA and can be ignored.
# The functionality being warned about is not used by SPISEA.
/Users/abhimat/Software/miniforge3/envs/phoebe_py38/lib/python3.8/site-packages/pysynphot/locations.py:345: UserWarning: Extinction files not found in /Volumes/Noh/models/cdbs/extinction
warnings.warn('Extinction files not found in %s' % (extdir, ))
Set up observation filters / passbands#
For this example, let’s generate photometry and RVs in HST’s WFC3IR F153M and F127M passbands.
filter_153m = filters.hst_f153m_filt()
filter_127m = filters.hst_f127m_filt()
Set up stellar and binary system parameters#
Set up isochrone object#
We’re going to set up parameters for the component stars interpolated from a MIST isochrone. Let’s choose an isochrone for an old star population located at the Galactic center…
Let’s walk through all the keywords:
age=8e9specifies an 8 Gyr old isochrone to be usedmet=0.0specifies an [M/H] = 0 metallicity (i.e. solar)use_atm_func='merged'specifies which atmosphere model to use from SPISEA. Here we use the merged atmosphere model. The atmosphere models available in SPISEA are detailed more here.phase='RGB'specifies to cut out stars on the isochrone that are identified to be on the Red Giant Branch only.ext_Ks=2.3specifies the K_s band extinction to derive synthetic photometry with SPISEA for the isochrone stars.dist=8e3*u.pcspecifies the distance where we want the synthetic photometry derived. Here we specify 8 kpc for the Galactic center. Changing this does not affect the output synthetic flux for Phitter’s binaries, and those can be modified later.filts_list=[filter_153m, filter_127m]specifies the list of filters for SPISEA to derive the synthetic fluxes. This should include all filters where fluxes are being simulated.ext_law='NL18'specifies the extinction law to use when deriving synthetic photometry. Here we useNL18referring to Nogueras-Lara+ 2018.
Phitter and SPISEA will now generate two isochrone objects with synthetic photometry. One at 10 pc with no extinction (for absolute magnitudes) and one at the target distance and extinction. This process can take a few minutes but the resulting isochrones are saved in the working directory and can be reused later.
# Object for interpolating stellar parameters from an isochrone
isoc_stellar_params_obj = isoc_interp_params.isoc_mist_stellar_params(
age=8e9,
met=0.0,
use_atm_func='merged',
phase='RGB',
ext_Ks=2.2,
dist=8e3*u.pc,
filts_list=[filter_153m, filter_127m],
ext_law='NL18',
)
Since we are using the red giant branch stars in this isochrone, we can select for stars by specifying a stellar radius. Along the red giant branch, we can typically uniquely select a star using radius. Here Phitter will interpolate all other stellar parameters based on the specified stellar radii of our component stars.
star1_params = isoc_stellar_params_obj.interp_star_params_rad(
15,
)
print("== Star 1 Parameters")
print(star1_params)
star2_params = isoc_stellar_params_obj.interp_star_params_rad(
12,
)
print("== Star 2 Parameters")
print(star2_params)
== Star 1 Parameters
mass_init = 1.103 solMass
mass = 1.100 solMass
rad = 15.000 solRad
lum = 70.325 solLum
teff = 4315.7 K
logg = 2.127
syncpar = 1.000
---
filt <phitter.filters.hst_f153m_filt object at 0x105016940>:
mag = 17.457
mag_abs = -1.909
pblum = 0.975 solLum
filt <phitter.filters.hst_f127m_filt object at 0x105016f40>:
mag = 20.483
mag_abs = -1.431
pblum = 1.181 solLum
== Star 2 Parameters
mass_init = 1.102 solMass
mass = 1.100 solMass
rad = 12.000 solRad
lum = 49.434 solLum
teff = 4418.1 K
logg = 2.321
syncpar = 1.000
---
filt <phitter.filters.hst_f153m_filt object at 0x105016940>:
mag = 17.883
mag_abs = -1.483
pblum = 0.659 solLum
filt <phitter.filters.hst_f127m_filt object at 0x105016f40>:
mag = 20.887
mag_abs = -1.028
pblum = 0.815 solLum
The remainder of the binary set up and calculation of simulated observables is similar to before.
Set up a binary parameters object#
# Binary parameters
bin_params = binary_params.binary_params(
period = 30.0 * u.d,
ecc = 0.2,
inc = 80.0 * u.deg,
t0 = 53_800.0,
)
Set up of observables to be calculated#
We need to set up an observables object to specify the times and types of observables that need to be computed. For this example, let’s compute flux in Keck K-band and RVs uniformly over the entire orbital phase of the binary.
# Set up model times
# Model times are in MJD here
model_phases = np.linspace(0, 1, num=100)
model_times = model_phases * bin_params.period.value + bin_params.t0
# Set up filter and observation type arrays for the model fluxes and RVs
flux_153m_filt_arr = np.full(len(model_phases), filter_153m)
flux_153m_type_arr = np.full(len(model_phases), 'phot')
flux_127m_filt_arr = np.full(len(model_phases), filter_127m)
flux_127m_type_arr = np.full(len(model_phases), 'phot')
rv_pri_filt_arr = np.full(len(model_phases), filter_153m)
rv_pri_type_arr = np.full(len(model_phases), 'rv_pri')
rv_sec_filt_arr = np.full(len(model_phases), filter_153m)
rv_sec_type_arr = np.full(len(model_phases), 'rv_sec')
# Now make arrays for all the times, filters, and observation types by concatenating the above arrays
obs_times = np.concatenate(
(model_times, model_times, model_times, model_times),
)
obs_filts = np.concatenate(
(flux_153m_filt_arr, flux_127m_filt_arr, rv_pri_filt_arr, rv_sec_filt_arr,),
)
obs_types = np.concatenate(
(flux_153m_type_arr, flux_127m_type_arr, rv_pri_type_arr, rv_sec_type_arr,),
)
# Finally, construct the observables object
model_observables = observables.observables(
obs_times=obs_times,
obs_filts=obs_filts, obs_types=obs_types,
)
Compute the observables#
Observables are computed as before. However, one difference here is that we can specify use_blackbody_atm=False which will allow PHOEBE to calculate photometry with Phoenix or Castelli and Kurucz model atmospheres rather than with a blackbody atmosphere.
# Object to perform the computation of flux and RVs
binary_model_obj = model_obs_calc.binary_star_model_obs(
model_observables,
use_blackbody_atm=False,
print_diagnostics=False,
)
The modeled observables can then be simulated by inputting the stellar and binary parameters.
modeled_observables = binary_model_obj.compute_obs(
star1_params, star2_params, bin_params,
)
Process and plot the modeled observables#
Note that the mags here are Absolute mags. By default, Phitter’s simulated output fluxes are absolute mags in a given passband.
# Fluxes in mags
modeled_mags_153m = modeled_observables.obs[modeled_observables.phot_filt_filters[filter_153m]]
print(f'F153M-band mags: {modeled_mags_153m}')
modeled_mags_127m = modeled_observables.obs[modeled_observables.phot_filt_filters[filter_127m]]
print(f'F127M-band mags: {modeled_mags_127m}')
# RVs in km/s
modeled_rvs_star1 = modeled_observables.obs[modeled_observables.obs_rv_pri_filter]
modeled_rvs_star2 = modeled_observables.obs[modeled_observables.obs_rv_sec_filter]
print(f'Star 1 RVs: {modeled_rvs_star1} km/s')
print(f'Star 2 RVs: {modeled_rvs_star2} km/s')
F153M-band mags: [-2.07376567 -2.08993976 -2.07376567 -2.0991852 -2.15546044 -2.22491996
-2.29432003 -2.35605566 -2.40597907 -2.44065194 -2.45367517 -2.45532707
-2.45694645 -2.45838347 -2.45975778 -2.46113128 -2.46246321 -2.46355262
-2.46466413 -2.46551129 -2.46661306 -2.46746037 -2.46813665 -2.46887976
-2.46934813 -2.46992754 -2.47032046 -2.47075715 -2.47111439 -2.47116211
-2.47125951 -2.47146599 -2.47156202 -2.47144126 -2.47138685 -2.47122224
-2.4710011 -2.47067124 -2.47037411 -2.46992726 -2.46946711 -2.46882896
-2.46829054 -2.46757638 -2.46683257 -2.46607895 -2.46515359 -2.46414984
-2.46315754 -2.46204834 -2.46092315 -2.45969034 -2.45854065 -2.45706278
-2.45585042 -2.45425752 -2.45295641 -2.43933153 -2.40171927 -2.34732274
-2.28018805 -2.20541217 -2.13148578 -2.07237965 -2.04551215 -2.06079345
-2.11251267 -2.1830001 -2.25757472 -2.32613203 -2.38318912 -2.42531764
-2.44893931 -2.45376083 -2.45831062 -2.46348046 -2.46939025 -2.47568068
-2.48202544 -2.48831559 -2.49376575 -2.49793381 -2.50065025 -2.50143559
-2.50034338 -2.49730215 -2.49264282 -2.48698856 -2.480567 -2.47378547
-2.46718838 -2.46100953 -2.45576449 -2.45046806 -2.42884237 -2.39063833
-2.33887726 -2.27620657 -2.20714624 -2.14024233]
F127M-band mags: [-1.61029623 -1.62663852 -1.61029623 -1.6358076 -1.69236212 -1.76215011
-1.83174369 -1.89339615 -1.94295009 -1.97704608 -1.98969145 -1.991178
-1.99262742 -1.99389067 -1.995116 -1.9963313 -1.99752277 -1.9984585
-1.99943488 -2.00015402 -2.00112902 -2.00186989 -2.00244946 -2.00309186
-2.00346717 -2.00397875 -2.00429888 -2.00467477 -2.00495985 -2.00496719
-2.00502061 -2.00518325 -2.00526509 -2.00513824 -2.00506564 -2.00490904
-2.00468997 -2.00437908 -2.00410685 -2.00369562 -2.00327324 -2.00268483
-2.00220894 -2.00155544 -2.00088769 -2.00022402 -1.99938824 -1.99848681
-1.9976092 -1.9966183 -1.99562672 -1.9945315 -1.99353002 -1.99219404
-1.99114931 -1.98971947 -1.9885937 -1.97502378 -1.93688921 -1.88109288
-1.81178367 -1.73429714 -1.65765666 -1.59648019 -1.56870949 -1.58448922
-1.63805517 -1.71128967 -1.78887502 -1.86011626 -1.91920457 -1.9625175
-1.9865371 -1.99139327 -1.99594195 -2.00110355 -2.0069787 -2.01325522
-2.01956889 -2.02586643 -2.03135186 -2.03557172 -2.03838394 -2.03929201
-2.03833485 -2.03543336 -2.03091259 -2.02538485 -2.01905831 -2.01233145
-2.00576286 -1.99957858 -1.9942999 -1.9889204 -1.96743857 -1.92933243
-1.87744592 -1.81440613 -1.74479348 -1.67735338]
Star 1 RVs: [ 8.96024086 2.97751958 -1.39149639 -4.21128267 -6.09344816
-7.5183564 -8.8026365 -10.18734265 -12.04716593 -14.17764211
-16.18991268 -18.09975825 -19.89607594 -21.58312924 -23.17086209
-24.65291747 -26.0322593 -27.31479824 -28.49566213 -29.58421983
-30.57638853 -31.48088871 -32.29518447 -33.0157848 -33.65197489
-34.20112844 -34.66339391 -35.04120352 -35.3371882 -35.54753077
-35.67686475 -35.72245268 -35.68198257 -35.56143318 -35.35962008
-35.07093973 -34.69899518 -34.24248534 -33.69986432 -33.06749555
-32.35266198 -31.54534657 -30.64944889 -29.6586031 -28.57184277
-27.39574907 -26.11709733 -24.73822599 -23.2579385 -21.67107733
-19.98379735 -18.18802279 -16.27909515 -14.26118298 -12.12920207
-9.88891019 -7.52917459 -5.05870009 -2.47672279 0.21543058
3.0094463 5.90776867 8.89393551 11.96827608 15.11012602
18.31058181 21.546962 24.80048393 28.04178532 31.24491701
34.37740099 37.3977694 40.26679173 42.94130402 45.38398488
47.54845591 49.39806855 50.90399364 52.04906128 52.81064614
53.18160126 53.16197407 52.75450554 51.96699174 50.80770409
49.29845861 47.45617257 45.31163347 42.89543312 40.24094938
37.39531831 34.41645618 31.90529969 29.74010527 27.72571683
25.6573344 23.22869333 19.92575285 15.1431524 8.96024086] km/s
Star 2 RVs: [ -8.95730242 -5.97482556 -3.08288617 -0.2911698 2.39978047
4.97957723 7.45210215 9.80974942 12.0583038 14.19236517
16.21592921 18.1279848 19.93144006 21.6244964 23.21596394
24.70345701 26.08612369 27.37265643 28.55939528 29.65072143
30.64559812 31.54753219 32.36080101 33.08216947 33.71641412
34.26392634 34.72487233 35.09893597 35.39125574 35.59523685
35.71834294 35.7586531 35.7137181 35.58581399 35.37533122
35.07850611 34.70000296 34.23405824 33.68181207 33.0447911
32.31875224 31.50433461 30.59606969 29.59791278 28.50495013
27.31746457 26.03279422 24.64694678 23.16235509 21.57226084
19.87879755 18.07803786 16.17169235 14.15472151 12.02468016
10.24656637 9.09500849 8.0965509 6.96559123 5.34313697
2.63092808 -2.01757293 -8.8063555 -15.89326698 -21.10352454
-24.35624001 -26.53371829 -28.28584588 -29.98835273 -31.88380026
-34.22173561 -37.19538834 -40.0688389 -42.76530832 -45.24034591
-47.45406972 -49.37433155 -50.96284924 -52.18731059 -53.02825494
-53.46522424 -53.48644931 -53.09644481 -52.29983376 -51.10968411
-49.55318678 -47.65469077 -45.45009213 -42.98386752 -40.28472383
-37.40464532 -34.38062868 -31.25383689 -28.05531361 -24.81956821
-21.57576276 -18.34787864 -15.1584592 -12.02461219 -8.95730242] km/s
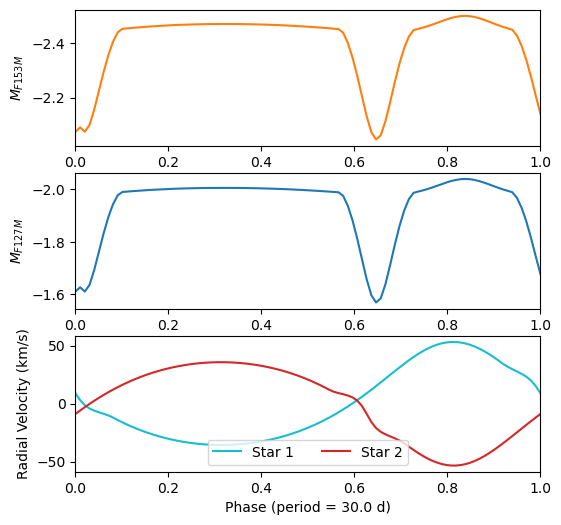
Now that we have the modeled observables, we can plot them for this model binary
fig = plt.figure(figsize=(6,6))
# F153M mags subplot
ax_mag_153m = fig.add_subplot(3,1,1)
ax_mag_153m.plot(
model_phases, modeled_mags_153m,
'-', color='C1',
)
ax_mag_153m.set_xlim([0, 1])
ax_mag_153m.invert_yaxis()
ax_mag_153m.set_ylabel(r"$M_{F153M}$")
# F153M mags subplot
ax_mag_127m = fig.add_subplot(3,1,2)
ax_mag_127m.plot(
model_phases, modeled_mags_127m,
'-', color='C0',
)
ax_mag_127m.set_xlim([0, 1])
ax_mag_127m.invert_yaxis()
ax_mag_127m.set_ylabel(r"$M_{F127M}$")
# RVs subplot
ax_rvs = fig.add_subplot(3,1,3)
ax_rvs.plot(
model_phases, modeled_rvs_star1,
'-', color='C9', label='Star 1',
)
ax_rvs.plot(
model_phases, modeled_rvs_star2,
'-', color='C3', label='Star 2',
)
ax_rvs.set_xlabel(f"Phase (period = {bin_params.period:.1f})")
ax_rvs.set_xlim([0, 1])
ax_rvs.set_ylabel("Radial Velocity (km/s)")
ax_rvs.legend(loc='lower center', ncol=2)
<matplotlib.legend.Legend at 0x15d0e5cd0>
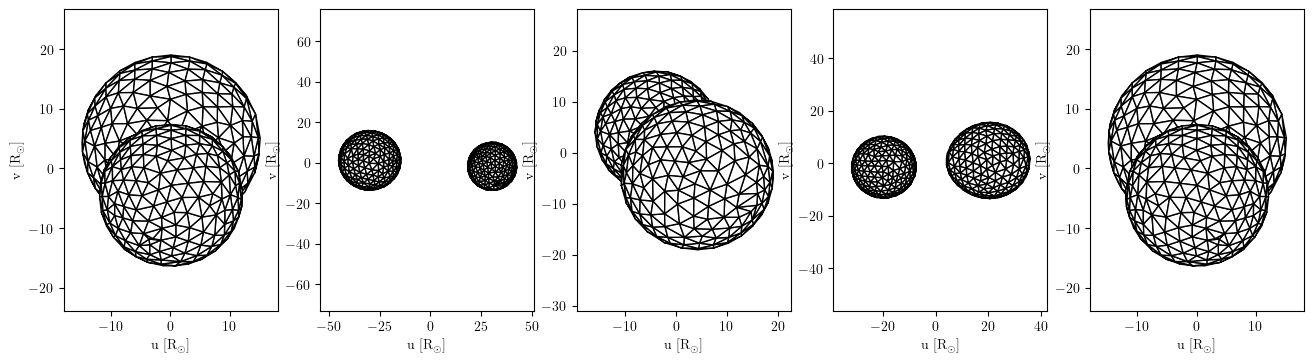
Bonus: make mesh plots to aide visualization#
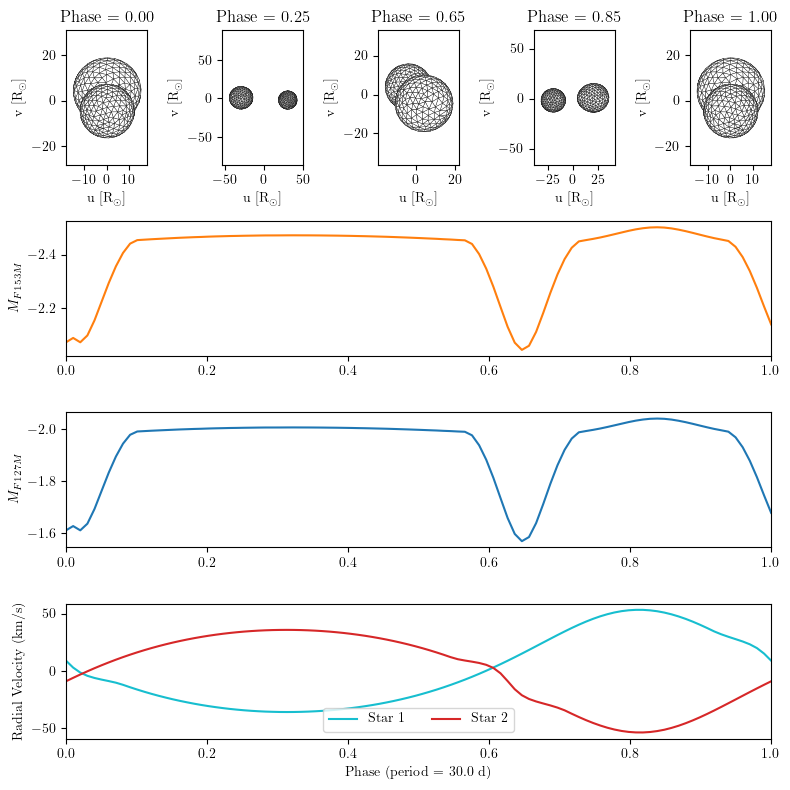
Once again, we can add some panels for mesh visualizations of the stars. For this eccentric binary example, we can change the phase values for where to draw the meshes. Photometric max happens at ~0.85 and an eclipse happens at ~0.65 so let’s include those.
# Set up figure and specificy mesh plot outputs
fig = plt.figure(figsize=(8,8))
mesh_plot_phases = np.array([0.0, 0.25, 0.65, 0.85, 1.0])
modeled_observables, mesh_plot_out, fig = binary_model_obj.compute_obs(
star1_params, star2_params, bin_params,
make_mesh_plots=True,
mesh_plot_phases=mesh_plot_phases,
mesh_plot_fig=fig,
mesh_plot_subplot_grid=(4,5),
mesh_plot_subplot_grid_indexes=np.array([1, 2, 3, 4, 5,]),
num_triangles=500,
)
# The mesh subplots show here since we have matplotlib inline enabled
# Finish constructing the whole figure
# Fluxes in mags
modeled_mags = modeled_observables.obs[modeled_observables.phot_filt_filters[filter_153m]]
# RVs in km/s
modeled_rvs_star1 = modeled_observables.obs[modeled_observables.obs_rv_pri_filter]
modeled_rvs_star2 = modeled_observables.obs[modeled_observables.obs_rv_sec_filter]
# Label the mesh subplots
# # Remove empty axes
# for ax in fig.axes:
# if ax.get_xlabel() == '':
# ax.remove()
# # Make mesh axes share axes
# mesh_axes = []
for ax_index, phase in enumerate(mesh_plot_phases):
ax = fig.axes[ax_index]
ax.set_title(f'Phase = {phase:.2f}')
# Decrease linewidths of the triangles in the mesh, for legibility in final plot
for child in ax.get_children():
if isinstance(child, mpl.collections.PolyCollection):
child.set(lw=0.25)
# mesh_axes.append(ax)
# Draw observables subplots
# F153m mags subplot
ax_mag_153m = fig.add_subplot(4,1,2)
ax_mag_153m.plot(
model_phases, modeled_mags_153m,
'-', color='C1',
)
ax_mag_153m.set_xlim([0, 1])
ax_mag_153m.invert_yaxis()
ax_mag_153m.set_ylabel(r"$M_{F153M}$")
# F127m mags subplot
ax_mag_127m = fig.add_subplot(4,1,3)
ax_mag_127m.plot(
model_phases, modeled_mags_127m,
'-', color='C0',
)
ax_mag_127m.set_xlim([0, 1])
ax_mag_127m.invert_yaxis()
ax_mag_127m.set_ylabel(r"$M_{F127M}$")
# RVs subplot
ax_rvs = fig.add_subplot(4,1,4)
ax_rvs.plot(
model_phases, modeled_rvs_star1,
'-', color='C9', label='Star 1',
)
ax_rvs.plot(
model_phases, modeled_rvs_star2,
'-', color='C3', label='Star 2',
)
ax_rvs.set_xlabel(f"Phase (period = {bin_params.period:.1f})")
ax_rvs.set_xlim([0, 1])
ax_rvs.set_ylabel("Radial Velocity (km/s)")
ax_rvs.legend(loc='lower center', ncol=2)
fig.set_size_inches(8, 8)
fig.tight_layout()
fig